백준 1463 JavaScript
문제
풀이
Dynamic-Programming으로 풀어야 한다. DP에 대해 처음 알게되어서 풀이를 검색해보니 다른 언어들은 재귀를 이용해 풀고 있었다. 하지만 자바스크립트에서 재귀를 사용하니 RangeError: Maximum call stack size exceeded 에러를 내뿜었다.
다른 방법이 필요해보였다.
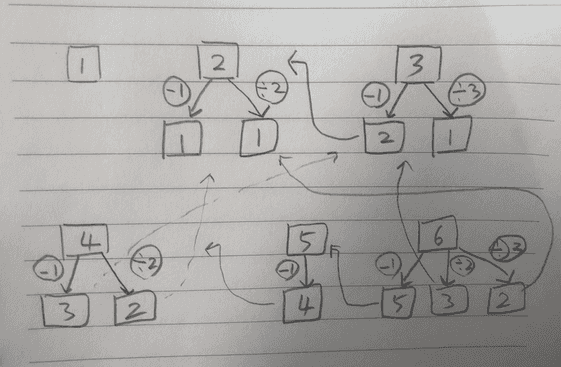
우선 재귀를 이용해 계산을 한다면, 정수 N에 대해 3으로 나누어 떨어지는 경우, 2로 나누어 떨어지는 경우, 그리고 -1을 빼는 경우를 계속 재귀시키고 이미 계산한 경우에는 메모이제이션을 적용해 다시 계산하지 않고 배열에서 불러온다.
const readFileSyncPath = '/dev/stdin';let N = parseInt(require('fs').readFileSync(readFileSyncPath).toString().trim());let dp = Array.from({ length: N + 1 }, (v, i) => null);dp[0] = dp[1] = 0;console.log(recur(dp, N));function recur(dpArr, num) {if (dpArr[num] === null) {if (num % 6 === 0) {dpArr[num] = Math.min(recur(dpArr, num - 1), Math.min(recur(dpArr, num / 3), recur(dpArr, num / 2))) + 1;} else if (num % 3 === 0) {dpArr[num] = Math.min(recur(dpArr, num / 3), recur(dpArr, num - 1)) + 1;} else if (num % 2 === 0) {dpArr[num] = Math.min(recur(dpArr, num / 2), recur(dpArr, num - 1)) + 1;} else {dpArr[num] = recur(dpArr, num - 1) + 1;}}return dpArr[num];}
하지만 위와 같이 코드를 작성하게 되면 앞서 말한 것처럼 런타임 에러 (StackSizeExceeded)가 발생한다.
종만북을 펼쳐보니 "반복적 동적 계획법"을 알게 되었다. 부분 문제 간의 의존성을 파악하기 쉬울 경우에 재귀 함수가 아니라 반복문을 이용해 동적 계획법을 구현할 수도 있다.
이 문제 같은 경우에는 입력 조건이 1보다 크거나 같고 10⁶보다 작거나 같은 정수 N이니, 2부터 정수 N까지 값을 계산해간다면 필요한 값들은 항상 가지고 있게 된다. 결과적으로 재귀 호출을 하지 않고 반복문을 사용해서 답을 계산할 수가 있다.
const readFileSyncPath = require('path').basename(__filename).replace(/js$/, 'txt');// const readFileSyncPath = '/dev/stdin';const N = parseInt(require('fs').readFileSync(readFileSyncPath).toString().trim());const DP = Array.from({ length: N + 1 }, i => 0);DP.forEach((v, i) => {DP[i] = DP[i - 1] + 1;if (i % 2 === 0) {DP[i] = Math.min(DP[i], DP[i / 2] + 1);}if (i % 3 === 0) {DP[i] = Math.min(DP[i], DP[i / 3] + 1);}});console.log(DP[N]);
반복문의 현재 값에 해당하는 연산 횟수는 처음에 이전 값의 횟수에 1을 더해 초기화 해준다. 정수 X에 사용할 수 있는 연산 중 "1을 뺀다"가 있기 때문에 그 연산 횟수에 1을 더한 값을 우선 가지고 있는 것이다. 그 다음에 2로 나누어 떨어지거나 3으로 나누어 떨어졌을 때의 값과 비교해서 작은 값으로 할당한다. 그렇게 해야 연산 횟수의 최솟값을 얻을 수 있다.